Welcome to Dental Clinic
A descriptive paragraph that tells clients how good you are and proves that you are the best choice that they’ve made. This paragraph is also for those who are looking out for a reliable dental clinic.
New Patient
A descriptive paragraph that tells clients how good you are and proves that you are the best choice that they’ve made. This paragraph is also for those who are looking out for a reliable dental clinic.
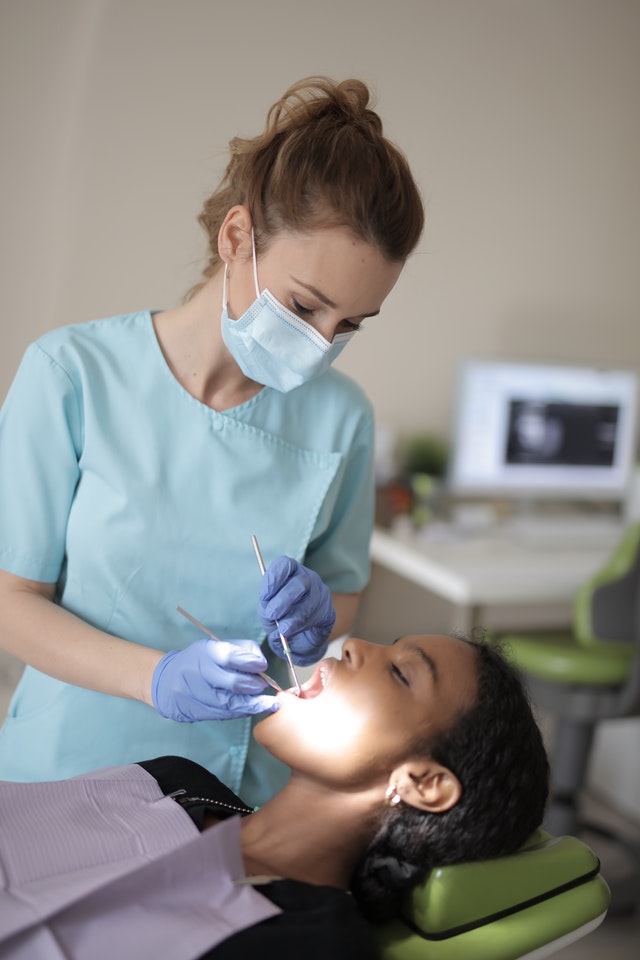
Dr. Michael Martinez
Master of Dentistry
Complete Care on Your Schedule
Bringing Life to Your Smile
Dentistry for Today’s Lifestyle
We Have All Your Dental Needs Covered
Happy Stories
Creating Vibrant Smiles for Healthy Lifestyles!
Voluptatum aspernatur ullamcorper hymenaeos. Saepe pretium voluptas ut velit augue, eget.Recusandae rerum, mus commodo tempora deserunt, nesciunt congue quod torquent suspendisse mauris.Voluptatem doloribus nihil !
Voluptatum aspernatur ullamcorper hymenaeos. Saepe pretium voluptas ut velit augue, eget.Recusandae rerum, mus commodo tempora deserunt, nesciunt congue quod torquent suspendisse mauris.Voluptatem doloribus nihil !
Voluptatum aspernatur ullamcorper hymenaeos. Saepe pretium voluptas ut velit augue, eget.Recusandae rerum, mus commodo tempora deserunt, nesciunt congue quod torquent suspendisse mauris.Voluptatem doloribus nihil !
Voluptatum aspernatur ullamcorper hymenaeos. Saepe pretium voluptas ut velit augue, eget.Recusandae rerum, mus commodo tempora deserunt, nesciunt congue quod torquent suspendisse mauris.Voluptatem doloribus nihil !
Voluptatum aspernatur ullamcorper hymenaeos. Saepe pretium voluptas ut velit augue, eget.Recusandae rerum, mus commodo tempora deserunt, nesciunt congue quod torquent suspendisse mauris.Voluptatem doloribus nihil !